Quando calculamos a órbita da Terra em torno do Sol, omitimos, de nossas equações, todos os outros planetas. No entanto, a atração de Júpiter, por exemplo, causa pequenas alterações na órbita terrestre. Para fazer uma estimativa dessas pequenas correções, elaborou-se um método, na mecânica celeste, que permitia a utilização, como ponto de partida, da órbita terrestre não perturbada, isto é, calculada omitindo-se Júpiter, calculando-se diretamente as modificações que deviam ser introduzidas na órbita não-perturbada. O aperfeiçoamento dessa técnica levou até mesmo à descoberta de novos planetas (Netuno, por exemplo, “traído” pela perturbação que causava na órbita de Urano).
A mecânica quântica tomou emprestada à mecânica celeste essa ideia, e surgiu assim a teoria das perturbações, que visa, a partir da solução conhecida de certos problemas, obter uma solução aproximada de problemas que, em algum sentido, são próximos ao problema resolvido. A teoria quântica das perturbações, porém, é muito mais simples do que aquela clássica.
Perturbação de estados estacionários
Seja ![]() um hamiltoniano cujo problema de autovalores já resolvemos. Conhecemos, então, as funções
um hamiltoniano cujo problema de autovalores já resolvemos. Conhecemos, então, as funções ![]() e os números
e os números ![]() tais que
tais que

Seja agora ![]() um novo hamiltoniano, muito próximo de
um novo hamiltoniano, muito próximo de ![]() , no seguinte sentido: todos os elementos de matriz
, no seguinte sentido: todos os elementos de matriz ![]() , em relação à base formada pelas
, em relação à base formada pelas ![]() , são pequenos em relação aos
, são pequenos em relação aos ![]() Diz-se então que
Diz-se então que ![]() é uma perturbação, que
é uma perturbação, que ![]() é o hamiltoniano perturbado, e que
é o hamiltoniano perturbado, e que ![]() é o hamiltoniano não-perturbado. É intuitivo que, nessas condições, os autovalores de
é o hamiltoniano não-perturbado. É intuitivo que, nessas condições, os autovalores de ![]() sejam próximos dos de
sejam próximos dos de ![]() , o mesmo acontecendo para as autofunções. Procuraremos simplificar a determinação das quantidades associadas a
, o mesmo acontecendo para as autofunções. Procuraremos simplificar a determinação das quantidades associadas a ![]() utilizando o fato de que elas são correções às quantidades associadas a
utilizando o fato de que elas são correções às quantidades associadas a ![]() .
.
O problema de autovalores de ![]() se escreve
se escreve

Como o conjunto dos ![]() é completo, existe a expansão
é completo, existe a expansão

e a Eq.(482) pode ser escrita

ou

Vamos usar agora a ortonormalidade dos ![]() . Multiplicando (483) à esquerda por
. Multiplicando (483) à esquerda por ![]() e integrando, temos:
e integrando, temos:

Mas
e
Logo,

ou

que é uma equação exata! Vamos agora introduzir as aproximações.
Uma condição básica para o que segue é que cada nível perturbado esteja muito próximo de um único nível não-perturbado, de sorte que![]() seja muito próximo de
seja muito próximo de ![]() , etc. Ou seja,
, etc. Ou seja,

onde os pontos denotam termos muito menores. Na expansão

teremos então



Usando (491) e (492) na Eq.(488), temos

Tomemos ![]() . A Eq.(493), dá:
. A Eq.(493), dá:

ou

Tomando ![]() na Eq.(493), obtemos
na Eq.(493), obtemos

ou

O primeiro resultado importante é este: a primeira correção ao autovalor não perturbado ![]() , é o valor médio do potencial perturbado,
, é o valor médio do potencial perturbado, ![]() , na função de onda não perturbada correspondente àquele valor de
, na função de onda não perturbada correspondente àquele valor de ![]() .
.
A construção da função de onda perturbada ainda não é possível, pois temos apenas os ![]() para
para ![]() . Falta determinar
. Falta determinar ![]() . Veremos agora que
. Veremos agora que ![]() pode ser tomado igual a zero. De fato, temos
pode ser tomado igual a zero. De fato, temos

ou, usando os resultados já obtidos,
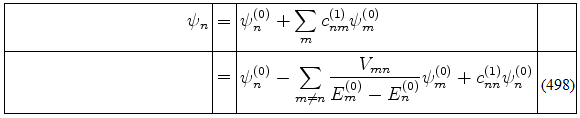
ou

Impondo que ![]() seja normalizada a menos de termos de segunda ordem, temos
seja normalizada a menos de termos de segunda ordem, temos

Logo,

ou

onde ![]() é um número real. Assim, o primeiro termo de (500) é
é um número real. Assim, o primeiro termo de (500) é

que, nesta ordem, é indistinguível de

Ou seja, o termo ![]() só contribui para uma mudança de fase de
só contribui para uma mudança de fase de ![]() , que, de qualquer forma, é definido a menos de uma fase. Logo, podemos legitimamente por
, que, de qualquer forma, é definido a menos de uma fase. Logo, podemos legitimamente por ![]() . Os resultados então são, até primeira ordem24,
. Os resultados então são, até primeira ordem24,

Exemplo trivial: Oscilador Harmônico com perturbação linear
Seja ![]() o hamiltoniano não-perturbado, e
o hamiltoniano não-perturbado, e
o hamiltoniano perturbado. Neste caso o problema de autovalores de ![]() , o hamiltoniano perturbado, pode ser resolvido exatamente, pois é essencialmente igual a
, o hamiltoniano perturbado, pode ser resolvido exatamente, pois é essencialmente igual a ![]() , com um diferente valor de
, com um diferente valor de ![]() . De fato, seus autovalores são
. De fato, seus autovalores são

com

É feita, adicionalmente, a hipótese de que
de maneira que

onde usamos o resultado de Newton (sim, Sir Isaac!):

para ![]() .
.
Logo, podemos escrever

e, portanto,

e, finalmente, lembrando que ![]() ,
,

Para o estado fundamental,

Vaos agora obter este mesmo resultado usando o formalismo perturbativo 25. Na notação perturbativa, temos, para o estado fundamental de ![]() ,
,

e

Temos

Logo,

que coincide com (514).
Correções de segunda ordem
Voltemos à Eq.(488):

e escrevamos a expansão de ![]() nas funções de onda não-perturbadas até segunda ordem:
nas funções de onda não-perturbadas até segunda ordem:

Analogamente, para as correções à energia , teremos:

Usando (520) e (521) em (519), temos

Igualando os termos de ordem zero:

Igualando os de ordem um:

E os de ordem 2:

As relações de ordem zero e um já foram exploradas. Vamos às de ordem 2. Para ![]() , temos, lembrando que
, temos, lembrando que ![]() ,
,

ou

e, lembrando que ![]() ,
,

FONTE: ©INSTITUTO DE FÍSICA DA UNIVERSIDADE DE SÃO PAULO – IF USP